時空の 3+1 分解 †
一般相対論の4次元時空は、適当に導入された時間座標一定の面にスライスされた3次元空間 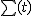 の時系列として捉える。これを、時空の 3+1分解 (正準形式, ADM形式)と呼ぶ。
の時系列として捉える。これを、時空の 3+1分解 (正準形式, ADM形式)と呼ぶ。
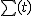 上の計量が
上の計量が
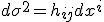 (
( 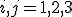 ) ・・・(1)
) ・・・(1)
のとき、4次元時空線素は
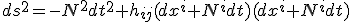 ・・・(2)
・・・(2)
と表せる。4次元計量テンソル10個のうち4つは座標によるパラメトリー化の自由度であり、力学的変数は6個になる。(2)は 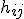 が6個になるように表現したものである。
が6個になるように表現したものである。
時空ダイナミクスを与えるアインシュタイン−ヒルベルト(Einstein-Hilbert)の作用積分は、表面積を除いて
![S_G=\frac{1}{{16}{\pi}{G}}\int{N}\sqrt{h}\left[{K^{ij}K_{ij}-K^2+^{(3)}R}\right]d^4x](cache/a7b3df27543c3ca1d4b30035538573df.mimetex.gif) ・・・(3)
・・・(3)
と表せる。ここで
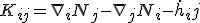 ・・・(4)
・・・(4)
は外部曲率と呼ばれ、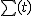 の埋め込みの仕方を与える。
の埋め込みの仕方を与える。
また、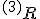 は
は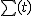 内でのスカラ曲率である。例えば、円柱面では
内でのスカラ曲率である。例えば、円柱面では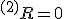 ,
, 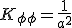 となり、固有曲率
となり、固有曲率 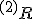 はゼロだが、3次元空間への埋め込み方に曲率がある(
はゼロだが、3次元空間への埋め込み方に曲率がある(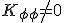 )ことを意味する。それに対して、球面では
)ことを意味する。それに対して、球面では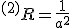 となり、固有曲率もゼロではない。
となり、固有曲率もゼロではない。
(3)のラグランジアンはラプス(lapse)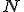 と
と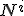 の時間微分を含まないので、これら4つの関数はダイナミクスの変数ではないことを意味する。
の時間微分を含まないので、これら4つの関数はダイナミクスの変数ではないことを意味する。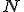 と
と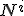 は座標系の選択に応じて決まるゲージ関数ということになる。
は座標系の選択に応じて決まるゲージ関数ということになる。
ロバートソン−ウォーカー計量(Robertson-Walker metric) †
宇宙モデルは、一様、等方3次元空間であり、その計量は定曲率空間として次のように表現される。
![d\sigma^2=a^2\left[{\frac{dx^2+dy^2+dz^2}{1+\frac{k}{4}r_1^2}}\right]](cache/583370c17310fcc51e2daa99307a9443.mimetex.gif) ・・・(5)
・・・(5)
![=a^2\left[{\frac{dr^2}{1-kr^2}+r^2(d\theta^2+\sin^2\theta d\phi^2)}\right]](cache/b24e0eb31c75bed569aa52764e707d54.mimetex.gif) ・・・(6)
・・・(6)
ここで 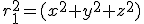 ,
, 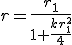 。
。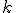 は曲率の符号を表し、
は曲率の符号を表し、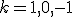 をとる。
をとる。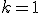 の場合
の場合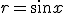 ,
, 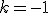 の場合
の場合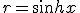 として、動径座標
として、動径座標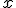 を導入すると(6)は
を導入すると(6)は
![d\sigma^2=a^2\left[{dx^2+f^2(x)(d\theta^2+\sin^2\theta\phi^2)}\right]](cache/f3ea584fe1ef0ed2f68239f0396f4d78.mimetex.gif) ・・・(7)
・・・(7)
と書ける。
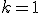 で
で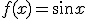 ,
, 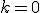 で
で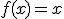 ,
, 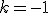 で
で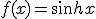 となる。
となる。
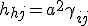 と書けば、定曲率空間の曲率は
と書けば、定曲率空間の曲率は
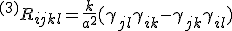 ・・・(8)
・・・(8)
であり、スカラテンソルは 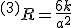 である。
である。
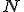 を
を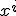 に依存しないようにとれば、
に依存しないようにとれば、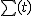 上の各点での固有時が同一になるので、そのような
上の各点での固有時が同一になるので、そのような 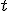 を宇宙時と呼ぶ。また、測地線方程式で
を宇宙時と呼ぶ。また、測地線方程式で 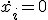 なら
なら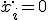 となるためには
となるためには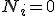 を取れば良い。
を取れば良い。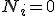 ととれば、
ととれば、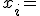 一定の世界線がテスト粒子の軌跡となり、このような座標系は物質に付随しているので共動座標と呼ぶ。世界時と共動座標を用いて(2)は次のように書ける。
一定の世界線がテスト粒子の軌跡となり、このような座標系は物質に付随しているので共動座標と呼ぶ。世界時と共動座標を用いて(2)は次のように書ける。
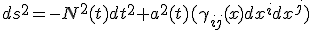 ・・・(9)
・・・(9)
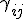 に(5)(6)(7)などと表せる定曲率空間の計量をとり、
に(5)(6)(7)などと表せる定曲率空間の計量をとり、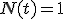 にとった計量(9)をロバートソン−ウォーカー計量(Robertson-Walker metrics)(R-W 計量)という。この計量は対称性と座標系の取り方によって決まるもので、一般相対論のダイナミクスは一切使われていない。
にとった計量(9)をロバートソン−ウォーカー計量(Robertson-Walker metrics)(R-W 計量)という。この計量は対称性と座標系の取り方によって決まるもので、一般相対論のダイナミクスは一切使われていない。
座標(7)でのR-W計量を用いて、動径方向 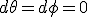 での光線の伝播は
での光線の伝播は
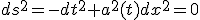 ・・・(10)
・・・(10)
で表せる。動径座標が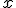 だけ離れた光源と観測者の間に
だけ離れた光源と観測者の間に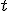 に発射した光が
に発射した光が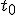 に受信され、
に受信され、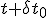 に受信されるとすれば、(10)より
に受信されるとすれば、(10)より
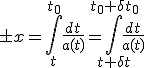 ・・・(11)
・・・(11)
ゆえに、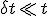 ならば
ならば
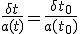 ・・・(12)
・・・(12)
と書ける。
空間ダイナミクスの運動方程式 †
R-W計量に対して作用積分(3)を書き下せば 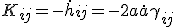 を用いて
を用いて
![S_{G}=\frac{1}{{16}{G}}\int Na^3\left[{3\frac{1}{a^4}(\frac{a\dot{a}}{N})^2+(\frac{3}{a^2}\frac{\dot{a}a}{N})^2+\frac{6k}{a^2}}\right]d^4x](cache/99228977c126a5edd09340ac2897c0c2.mimetex.gif)
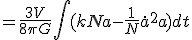 ・・・(13)
・・・(13)
ここで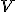 は空間座標について積分した体積。
は空間座標について積分した体積。
物質として共動座標に静止した媒質を考えたとき
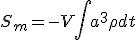 ・・・(14)
・・・(14)
全ラグランジアンは
![L=\frac{3}{8{\pi}{G}}\left[{kNa-\frac{1}{N}\dot{a}a}\right]-\rho Na^3](cache/d9c222aa10945598914b1df95d20b033.mimetex.gif) ・・・(15)
・・・(15)
運動方程式は オイラー−ラグランジュ(Euler-Lagrange)(E-L)方程式
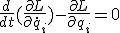 ・・・(16)
・・・(16)
より導かれる。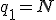 に対しては
に対しては
![\frac{3}{8{\pi}{G}}\left[{ka+\frac{1}{N^2}\dot{a}^2a}\right]-\rho a^3=0](cache/0390acc8cc1d8c9dd4fa80dc4cc140ed.mimetex.gif) ・・・(17)
・・・(17)
というハミルトン(Hamilton)の拘束条件が得られる。ここで 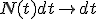 なる新しい時間座標をとれば、
なる新しい時間座標をとれば、
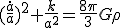 ・・・(a)
・・・(a)
この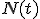 をとって、
をとって、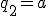 として(16)を用いると
として(16)を用いると
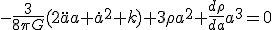 ・・・(18)
・・・(18)
となる。ここで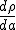 の項は熱力学第1法則を断熱過程に用いた式
の項は熱力学第1法則を断熱過程に用いた式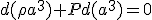 より
より
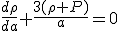 ・・・(19)
・・・(19)
であり、これを(18)に代入すると
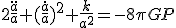 ・・・(b)
・・・(b)
となる。
(b)に(a)を適用すると
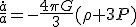 ・・・(c)
・・・(c)
(a)の右辺をエネルギー項と呼び、左辺第2項を曲率項と呼ぶ。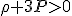 なら原則膨張となる。
なら原則膨張となる。
物質の典型例として「ダスト」(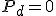 ), 「放射」(
), 「放射」(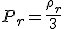 ), 「真空」(
), 「真空」(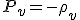 )を扱い、(19)より、各々
)を扱い、(19)より、各々
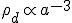 ,
, 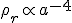 ,
, 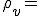 一定 ・・・(20)
一定 ・・・(20)
スカラ場 †
3次元空間で一様なスカラ場が存在する場合は(14)のかわりに
![S_{\phi}=V\int a^3\left[{\frac{\phi^2}{2N}-NV_{\Phi}(\Phi)}\right]dt](cache/f5bcf25f66e3cac8e35b966fb87f47ae.mimetex.gif) ・・・(21)
・・・(21)
となる。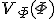 は真空エネルギー。
は真空エネルギー。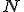 および
および についてのE-L方程式は、各々
についてのE-L方程式は、各々
![(\frac{\dot{a}}{a})+\frac{k}{a^2}=\frac{8{\pi}{G}}{3}\left[{\frac{1}{2}\Phi^2+V_{\Phi}(\Phi)}\right]](cache/01d7d388aae44ed3a35219e215465bdb.mimetex.gif) ・・・(22)
・・・(22)
![2(\frac{\ddot{a}}{a})+(\frac{\dot{a}}{a})^2+\frac{k}{a^2}=-8{\pi}{G}\left[{\frac{1}{2}\Phi^2-V_{\Phi}(\Phi)}\right]](cache/a3cdbf047ef09af096220662ffcd29de.mimetex.gif) ・・・(23)
・・・(23)
右辺を(a)(b)に対応させると
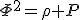 ,
, 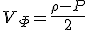 ・・・(24)
・・・(24)
また、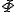 についてのE-L方程式より
についてのE-L方程式より
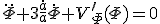 ・・・(25)
・・・(25)
ホイラー−ドウイット方程式(Wheeler- DeWitt? equation) †
ラグランジアン
![L=\frac{3}{8{\pi}{G}}\left[{ka-\dot{a}^2a}\right]+\left[{\frac{\dot{\Phi}^2}{2}-V_{\Phi}}\right]a^3](cache/e5c83cb5c13cb0007c79fd2a0c41c7fd.mimetex.gif) ・・・(26)
・・・(26)
からハミルトニアン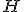 を
を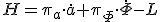 とすると
とすると
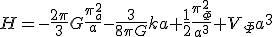 ・・・(27)
・・・(27)
ここで、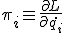 は運動量。
は運動量。
(17)に対応したハミルトンの拘束条件は 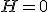 のことである。このハミルトニアン
のことである。このハミルトニアン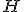 を
を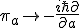 ,
, 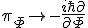 の置き換えを行ってオペレータとみなす。
の置き換えを行ってオペレータとみなす。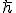 はプランク定数。
はプランク定数。
量子力学では 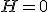 の条件を、状態
の条件を、状態 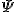 を拘束する
を拘束する
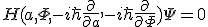 ・・・(28)
・・・(28)
という方程式に読み替える。これは拘束条件に関するディラックの量子化条件を適用したものである。
一般には、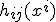 と
と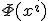 などの物質場の関数として与えられる
などの物質場の関数として与えられる
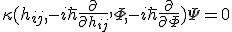 ・・・(29)
・・・(29)
という方程式をホイラー−ドウイット(Wheeler-DeWitt?)方程式と呼ぶ。(28)はその特殊な場合である。
簡単な場合をとり、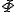 が
が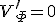 の位置
の位置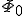 にとどまっているとして(28)を書き下すと
にとどまっているとして(28)を書き下すと
![\left[{\frac{d^2}{da^2}-V_{eff}(a)}\right]\Psi=0](cache/3802259f4e644d4e09c7661f69dd2f1c.mimetex.gif) ・・・(30)
・・・(30)
![V_{eff}=(\frac{3}{4{\pi}])^2\frac{1}{l_{Pl}^4}a^2(a-H^2a^2)](cache/1f8b1e2ec2ae7720930a7e932616e008.mimetex.gif) ,
, 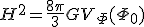 ・・・(31)
・・・(31)
ここで
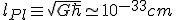 ・・・(32)
・・・(32)
はプランク長さである。
ド・ジッター(de Sitter)宇宙と埋め込み †
(未完成)
多重連結空間 †
(未完成)
参考 †
- 宇宙物理 [現代物理学叢書] 佐藤文隆/著 岩波書店(ISBN4-00-006756-7)
- 宇宙がわかる17の方程式 [現代物理学入門] Sander Bais/著(寺島英志/訳) 青土社(ISBN4-7917-6288-6)
- 物理小事典 第4版 三省堂(ISBN4-385-24016-7)
MLEXP. Wiki
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)